本文共 710 字，大约阅读时间需要 2 分钟。

计算函数的定积分

如果用每个小矩形面积的和，代替每个小梯形面积的和，以此来计算函数的定积: 其实计算方法会更简单，只是误差会变大，请推导这个计算公式，并用函数指针编写这个程序。

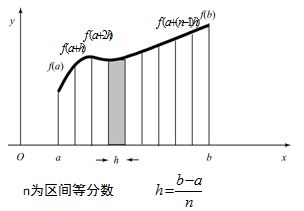
[注]使用矩形法推导函数定积分的计算公式是微积分上册十分经典的一个问题, 这里不再对推导过程赘述.

#include
   
    double Definite_Integral(double, double, double (*)(double), short);double f1(double);double f2(double);int main(){    double result;    printf("f1 = x / (1 + x ^ 2)\n");    printf("f2 = 1 + x ^ 2\n");    /* 对函数f2在区间[0, 3]上求定积分 */    result = Definite_Integral(0, 3, f1, 1000);    printf("result(f1在[0, 3]上做定积分运算) = %.6lf\n", result);    result = Definite_Integral(0, 1, f2, 1000);    printf("result(f2在[0, 1]上做定积分运算) = %.6lf\n", result);    /* */    return 0;}/* 计算函数的定积分 */double Definite_Integral(double a, double b, double (*f)(double), short n){    d
   

转载地址：http://edsg.baihongyu.com/